Damage Analysis of 710 mm2 ACCC Strands Considering the Contact and Friction Behavior between Strands
-
摘要: 利用扫描电镜观察710 mm2碳纤维复合芯导线(ACCC)过滑车试验后股线的磨损形貌，分析滑车底径对股线损伤的影响及股线损伤机制. 同时，考虑股线间的接触与摩擦行为，建立导线全尺寸模型进行导线过滑车非线性动力学有限元分析. 试验结果表明：导线过滑车后股线出现塑性变形与磨损，在股线表面初始磨损处以黏着磨损的形式扩展，且股线损伤随滑车底径的增大有所改善；数值分析表明：股线等效塑性应变与摩擦能量损耗开始于导线过滑车时的弯曲过程，且随滑车底径增大而减小，股线损伤的模拟结果与试验情况吻合. 在此基础上，研究股线间摩擦系数对股线损伤影响，得到股线损伤随摩擦系数的减小而减小. 研究初步认为滑车底径为30倍导线直径时股线损伤在可接受范围内.
-
关键词:
- 碳纤维复合芯导线(ACCC) /
- 股线损伤 /
- 滑车底径 /
- 接触 /
- 摩擦行为
Abstract: Worn surface morphologies of the tested 710 mm2 ACCC strands were observed by scanning electron microscopy, and the influence of the stringing block diameter on strands damage and mechanisms were analyzed. Considering the contact and friction between strands, the ACCC full-scaled model was built and nonlinear dynamics finite element analysis of ACCC after passing the stringing block was carried out. The test results show that the plastic deformation and wear appeared on the strand surface after test. Adhesive wear proceeded from the initial wear region on the strand surface, and strands damage was improved with the increase of the stringing block diameter. The numerical analysis indicates that PEEQ and frictional dissipation, which were started on the bending stage of strands, decreased with the increase of the stringing block diameter. The simulation result was in good agreement with the test result. Based on the above results, the influence of the friction coefficient between strands on the strands damage was studied, and the strands damage was improved with the decrease of the friction coefficients. Synthetically consideration, the strands damage was acceptable when the stringing block diameter was 30 times of the diameter of ACCC.-
Keywords:
- ACCC /
- strands damage /
- diameter of stringing block /
- contact /
- friction behavior
-
碳纤维复合芯导线(简称ACCC)具有强度高、损耗小、重量轻、弧垂小等优点，将逐步代替传统钢芯铝绞线成为节能架空导线的典型[1]. 软铝梯形股线为导线导体，导线在架线施工过滑车环节因机械性能差造成股线损伤将影响导线综合性能，因此股线力学性能研究不容忽视. Nawrocki等[2–3]研究了不同股线滑滚行为对绞线弯曲刚度影响. Jiang等[4]研究发现同层股线间发生接触. Raoof等[5]将绞线每层股线简化为各向异性圆筒，但该模型只适合研究绞线整体响应，不适合分析股线接触与摩擦行为、股线应力状态等局部响应. Zhou等[6–7]建立了单层股线绞线在弹性范围内的有限元模型，并未考虑股线间摩擦与滑移及拉伸载荷的影响. Fontanari等[8]研究了复合材料芯绞线弹塑性响应，但模型长度过小易产生边界效应. 考虑股线间接触与摩擦，Kmet等[9–10]分别建立了4层与6层股线绞线的有限元模型，但两者均未考虑弯曲载荷下的非线性行为. 目前有关ACCC芯棒力学研究较多[11–13]，但忽视了导线过滑车时股线复杂的力学分析.
导线过滑车时，股线在弯曲载荷作用下易产生塑性变形，因此滑车底径对股线损伤乃至对导线电性能影响很大. 利用试验方法研究滑车底径对股线损伤的试验成本高，且无法在理论上得到股线内部的力学响应. 因此本文中分析710 mm2 ACCC过不同底径滑车试验后的股线损伤及机理，并考虑股线间接触与摩擦行为，建立导线全尺寸模型进行非线性动力学有限元分析，理论上研究滑车底径对ACCC股线的损伤问题，并证明有限元模型的有效性，进而对滑车底径的选择提出合理化建议.
1. 导线过滑车试验研究
为保证导线顺利通过滑车且股线损伤在安全范围内，蒋平海[14]认为钢芯铝绞线用放线滑车底径不小于导线直径的20倍，电力行业标准[15]与企业标准[16]规定碳纤维复合芯导线用放线滑车底径分别为导线直径的30倍和40倍，标准中的规定出现了不一致现象，且未在理论上进行深入分析. 为探究滑车底径对碳纤维复合芯导线中股线的影响以及确定滑车的最优底径，本文中拟对710 mm2碳纤维复合芯导线(见图1)进行过滑车试验. 由图1可知，股线截面为梯形.
为模拟导线过滑车时的工况，依据导线过滑车试验要求制定试验方案[17]，将试验设备按图2搭建试验平台，加载装置提供导线一定张力，启动动力装置，使型号为JLRX1/F1A-710/70-325导线以6 m/min循环往复通过滑车20次. 导线与滑车的包络角α=30°，试验系统张力T为25%RTS(额定拉断力)，滑车底径分别为D=20 d、25 d、30 d、40 d(d为导线直径)，每个工况试验样本数为9.
![]()
图 2 导线过滑车试验照片与示意图Figure 2. Photograph and schematic diagram of ACCC passing the stringing block test2. 导线过滑车数值模拟
2.1 三维模型的生成
表1中列出了试验用710 mm2碳纤维复合芯导线的几何参数[17]. 利用SolidWorks三维建模软件建立螺旋股线与碳纤维芯棒的三维模型，并将其以环形阵列的方式装配[见图3(a)]. 为了避免边界效应影响仿真结果[8]，模型长度应至少大于螺旋股线的1个节距长度，本模型长度取L=1 000 mm.
表 1 710 mm2碳纤维复合芯导线几何参数[17]Table 1. Geometric parameter of 710 mm2 ACCCSample Numbers Diameter/mm Section shape Stranding direction Lay ratio Strands Inner 8 d1=17.5 Trapezoid Right 15.04 Mid 12 d2=25.16 Trapezoid Left 13.09 Outer 16 d3=32.8 Trapezoid Right 10.33 Core Carbon fiber 1 dc=6.8 Circular - - Glass fiber 1 dg=9.5 Circular - - 2.2 有限元模型的建立
ACCC属于螺旋非对称结构[见图3(a)]，需对导线的全尺寸模型进行分析. 为解决结果不收敛问题，利用ABAQUS/explicit模块的显示时间积分法对模型进行股线间复杂的接触与非线性分析[9, 18]，并建立如图3(b)所示的有限元模型. 分析中将滑车简化为圆筒，导线轴线与滑车呈15°相切关系，导线左端面与滑车槽接触，给导线施加沿自身轴向的预应力与初始速度，预应力大小可通过材料力学计算得到(49.2 MPa)，初始速度大小与滑车旋转的线速度相等. 滑车带动导线逆时针旋转，使存在轴向预应力的导线在滑车驱动下弯曲，形成如图2所示30°的包络角后停止计算. 此时弯曲段导线会同时受到拉伸载荷与弯曲载荷作用，达到与实际试验中导线更相近的受力状态.
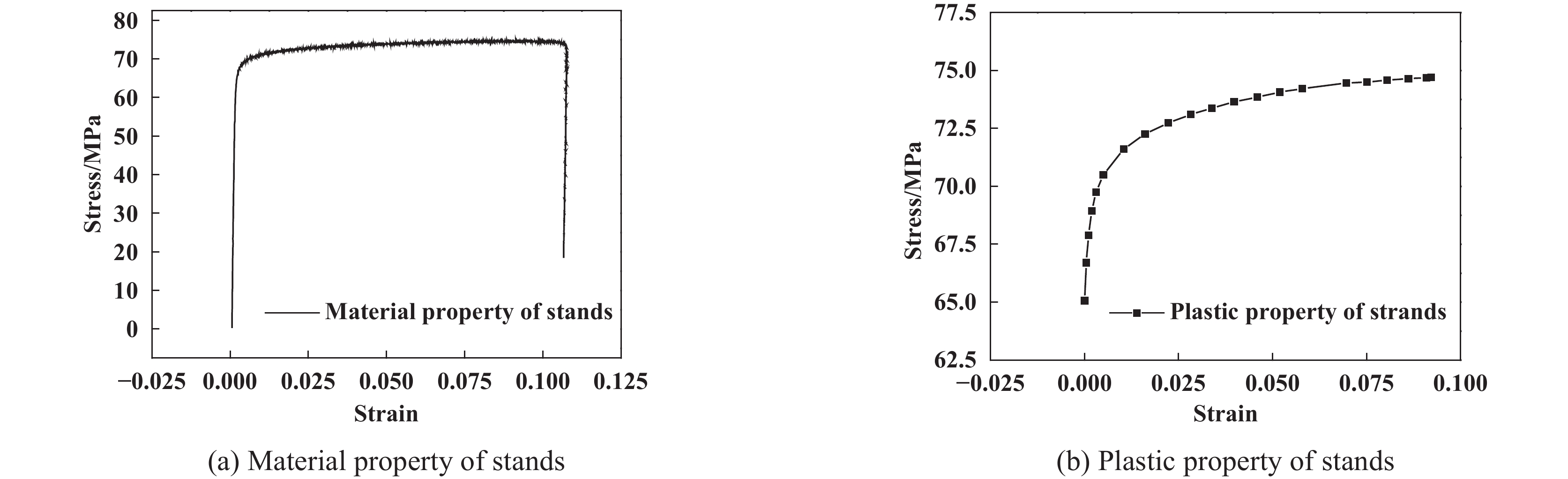
表2所示为ACCC材料属性，其中，软铝股线的应力-应变曲线由拉伸试验得到[19]，进而得到其塑性应力-应变曲线(见图4). 碳纤维芯棒的材料属性与文献[20]相同，简化为各项同性材料. 导线弯曲导致股线间相互作用，必须考虑股线间的接触与摩擦，各层股线交错分布导致接触面错综复杂，宜采用通用接触类型(General contact)并遵循库仑定律，摩擦系数大小根据分析条件而定. 为分析股线在拉伸与弯曲载荷作用下的接触与摩擦行为，模型采用减缩积分与沙漏控制的C3D8R单元，该方法可使单元在弯曲时不会有很大的刚度，在积分点的应力与应变结果会更加精确[9]，网格划分后的导线模型共70 464个节点，41 944个单元.
表 2 ACCC材料属性Table 2. Material parameter of 710 mm2 ACCCSample Parameter E/GPa σb/MPa σs/MPa μ Strands 44 75 65 0.3 Carbon fiber 147.9 3 144.6 - 0.25 Glass fiber 53.2 1 550.0 - 0.28 3. 结果与讨论
3.1 结果分析
试验后导线出现了不同程度的散股[见图5(a)]，即同层股线间相邻两股线相互分离，散股现象随滑车底径的增大明显减弱，这可归因于导线过滑车时产生的弯曲载荷导致股线出现的塑性变形所致，且股线所受弯曲载荷随滑车底径不同而不同，进而导致其塑性变形不同. 与此同时，邻层股线间的相互滑移导致股线表面产生摩擦磨损现象，尤其外层股线内表面对中层股线外表面的磨损最严重[见图5(b)]，且磨损程度随滑车底径的增大而减小，这可能是由于邻层股线间相对滑移量随所受弯曲半径的增大而减小所致.
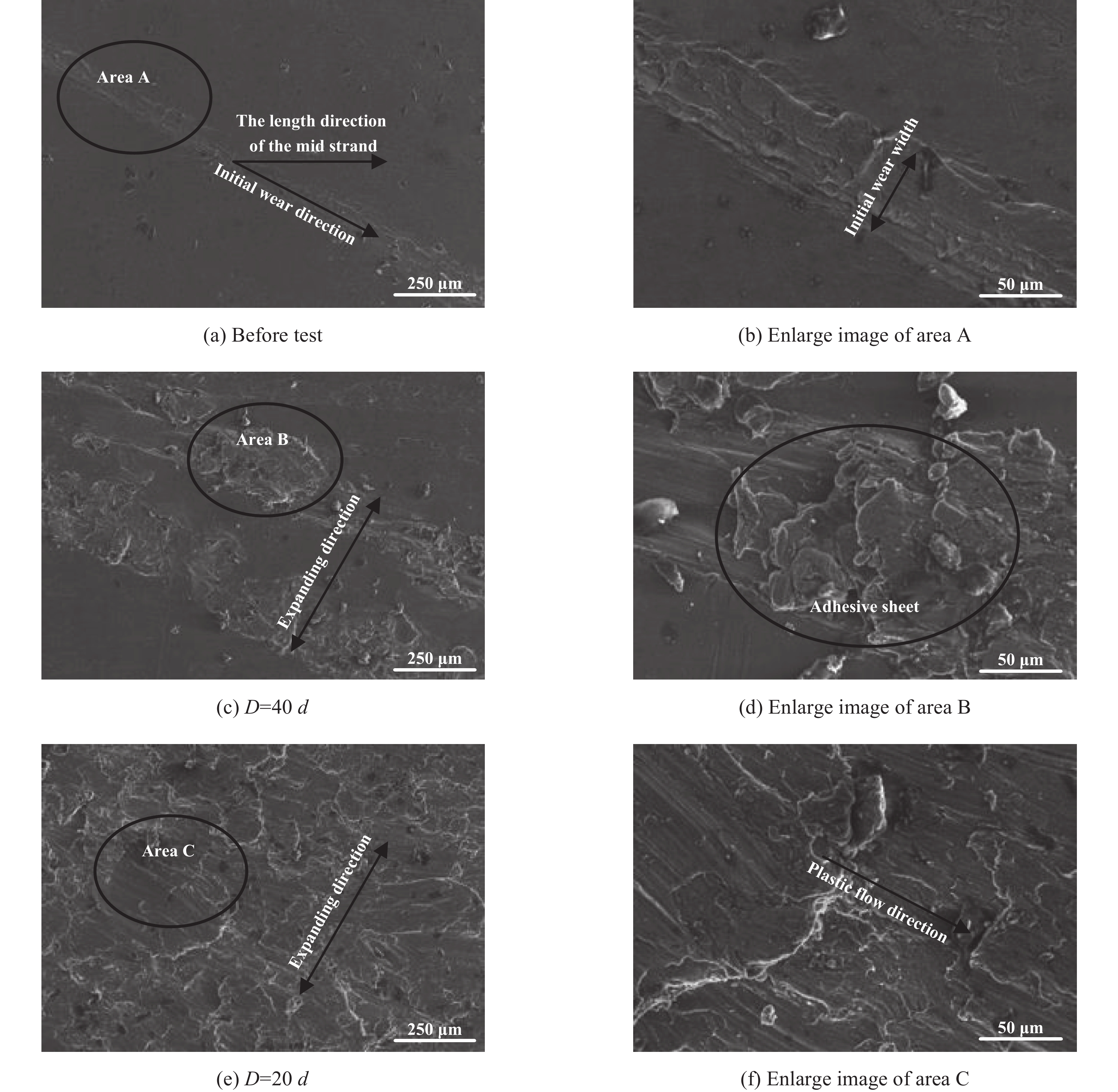
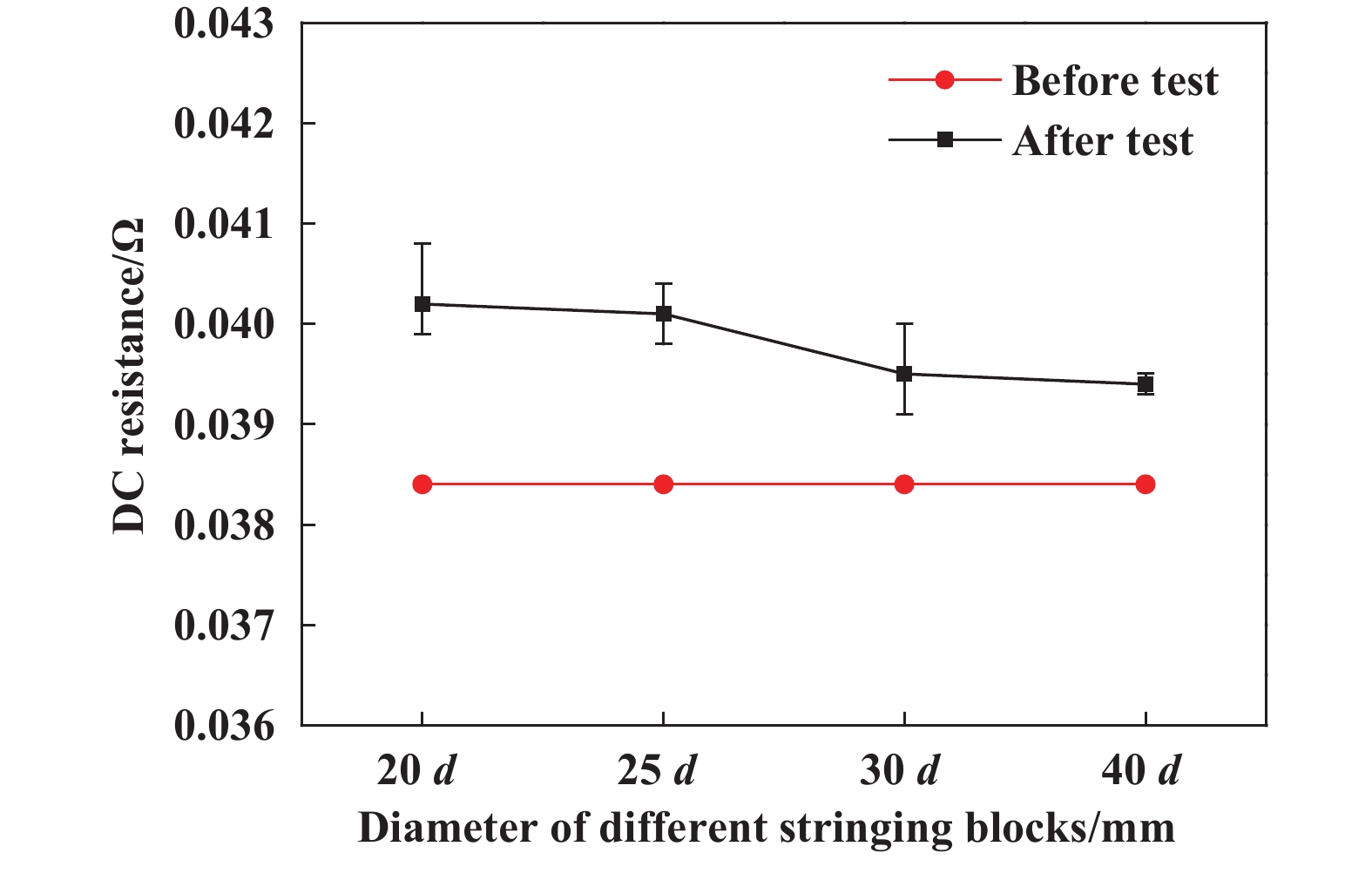
为分析股线的损伤机制，将图5(b)中的B、C、F放大后进行分析(见图6)，由图6(a~b)可知，股线在试验前已出现宽度约50 μm的初始磨损，磨损方向与上层股线绞制方向一致，且压痕在导线运输过程产生了微小塑性流动，这是因为导线在生产过程中，外层股线的快速绞制对中层股线外表面产生冲击绞制力所致. 如图6(c~d)所示，微区可见明显磨痕、金属片状剥落物的堆积，可判断此过程以黏着磨损为主，可能由于导线过滑车时股线在弯曲变形及滑移过程中发生高温软化造成局部塑性变形，进而由于接触面间的摩擦作用导致塑性变形区域剥落形成凹坑[21]. 如图6(e~f)所示，随着滑车底径的减小，股线间的变形与滑移不断增大，且导线循环通过滑车时股线在自身长度方向的塑性变形与宽度方向的反复滑移导致黏着磨损加剧扩展，股线表面在外层股线方向上出现严重塑性流动. 导线在架线施工或长期运行中易在股线磨损严重处断裂，造成工程事故，因此综合考虑股线损伤程度、导线20 ℃时直流电阻变化趋势(图7)与滑车轻量化的设计要求，初步认为滑车底径为30倍导线直径合适.
![]()
图 6 导线中层股线外表面磨痕图Figure 6. SEM micrographs of wear track in the outer surface of mid-layered strands3.2 有限元结果分析
3.2.1 滑车底径对股线损伤的影响
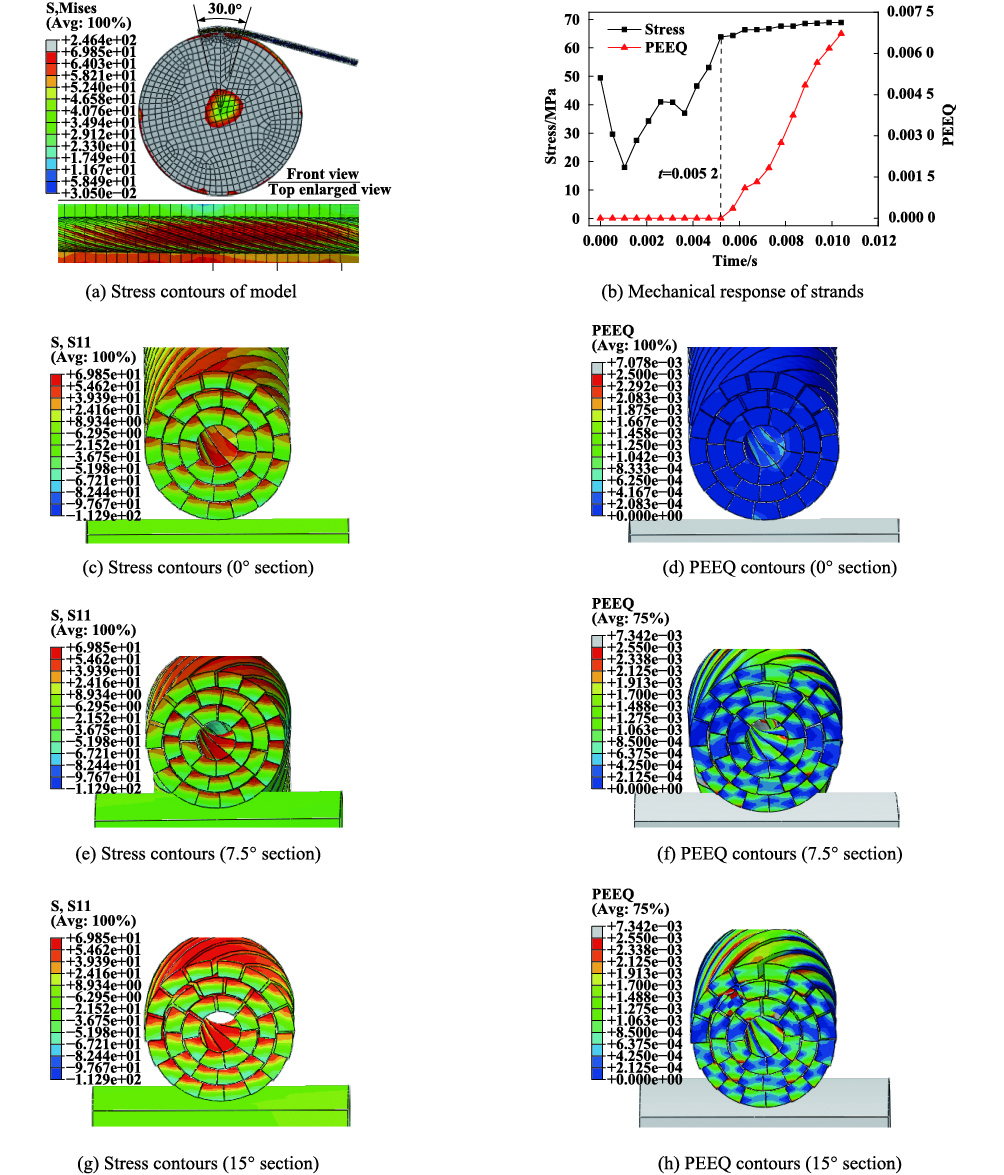
导线通过滑车时(以D=30 d为例)，滑车底径对股线损伤影响的分析结果如图8所示(本文中侧重分析股线力学行为，故在应力与应变云图中将碳纤维芯棒隐藏处理)，摩擦系数取μ=0.6，其他参数与试验条件相同. 由图8(a)可知，股线最大应力(69.1 MPa)出现在导线与滑车接触弧长的中部，且向两侧依次递减. 对此处的最大应力单元进行分析[图8(b)]可知，此单元在通过滑车前应力出现先减小后增大的浮动，这可归因于在导线运动过程中股线沿轴向与周向的滑移. 当此单元在t=0.005 2 s时开始进入滑车，并出现塑性变形. 当单元进入滑车转动15°到与滑车接触弧长的中部过程中应力缓慢增大(由63.9 MPa到69.1 MPa)，PEEQ (等效塑性应变)呈线性快速上升(由0%到0.73%)，图8(c~h)所示导线与滑车不同接触位置的截面应力与应变云图也论证了变化的趋势. 由此可见，导线进入滑车弯曲后，股线应力开始超过自身的屈服强度(对比表2)，股线出现塑性变形. 因此，研究碳纤维复合芯导线过滑车时的力学响应对预测导线损伤尤为重要.
![]()
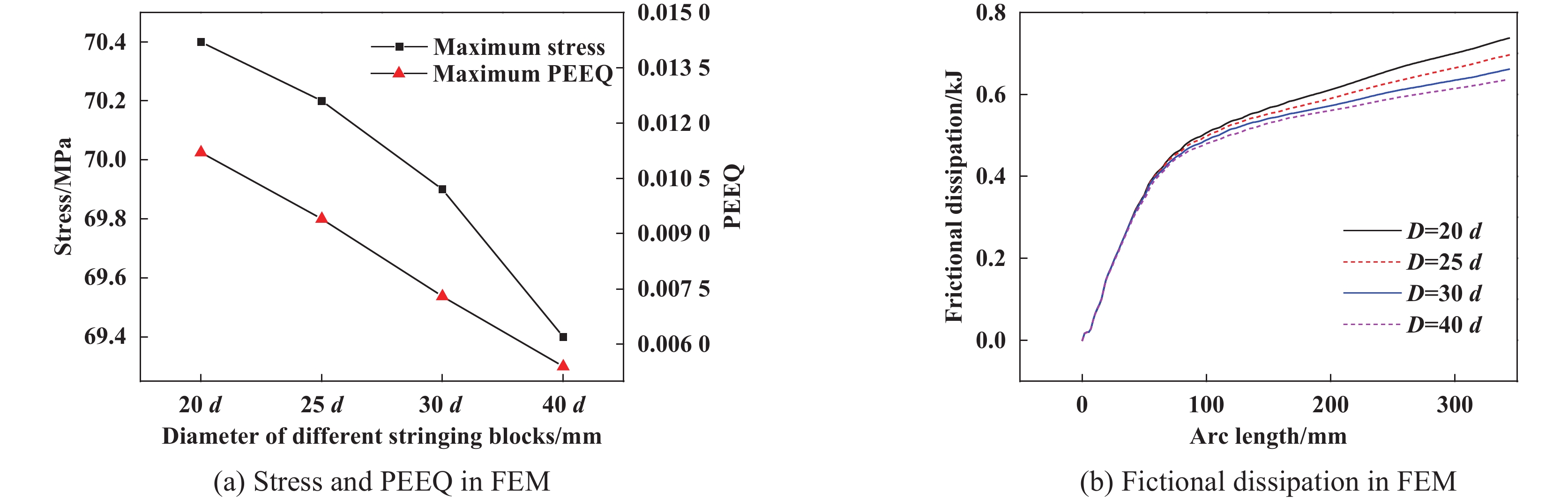
图 8 通过滑车时ACCC股线的力学响应(以D=30 d为例)Figure 8. Mechanical response of ACCC strands when passing the stringing block (D=30 d)由图8(c~h)中间截面沿绞线轴向的主应力与等效塑性应变(PEEQ)云图可知，应力与塑性应变均呈层状分布，同根股线中，上部应力大于下部应力，截面塑性变形区域呈从上到下逐渐减小的趋势，且左右两侧对称变化. 不同滑车底径下股线的力学响应如图9所示，由图9(a)可得到，过滑车后的股线最大应力均超过自身屈服强度，股线发生塑性变形，变形量随滑车底径的增大呈下降趋势. 同时，观察图8的股线截面可知，上部股线相互分离，下部股线相互挤压. 已知试验中可观察到导线过滑车时会由于自身的螺旋结构产生自转现象，因此当导线多次通过滑车时股线同截面与滑车槽的相对位置具有随机性，即同一位置的股线会在远离滑车槽端时相互分离而在接触滑车槽时相互挤压. 股线的塑性变形与反复滑移的运动方式使导线出现了散股问题与股线表面磨损. 利用有限元结果中的摩擦滑移能量损耗表征股线间相对滑移的磨损程度[22]，图9(b)为导线过不同滑车时股线摩擦能量损耗随导线进入滑车弧长变化的曲线，可知股线磨损程度随导线进入滑车的弧长增加而增加，随滑车底径的增大而减小，分析结果与图5的试验结果一致性较好. 试验分析中得到选用的滑车底径应是导线直径的30倍，因此，可将图8(h)中股线塑性变形单元占总单元数量的32.6%作为滑车底径选取的判据.
![]()
图 9 不同滑车底径下ACCC股线的力学响应Figure 9. Mechanical response of ACCC strands in different stringing blocks(D=30 d)3.2.2 摩擦系数对股线损伤的影响
ACCC导线在生产过程中可能因绞制力的冲击对股线表面产生初始压痕及损伤[见图6(b)]，在工程应用前的长期储存过程中，股线损伤表面可能因化学老化造成表面粗糙度变化，从而引起股线间摩擦系数的变化[22]. 本文作者在证明有限元模型预测有效性的基础上研究摩擦系数对股线损伤的影响. 假设摩擦系数μ为0.60、0.65、0.70和0.75，滑车底径取20 d、25 d、30 d和40 d，其余参数与试验一致.
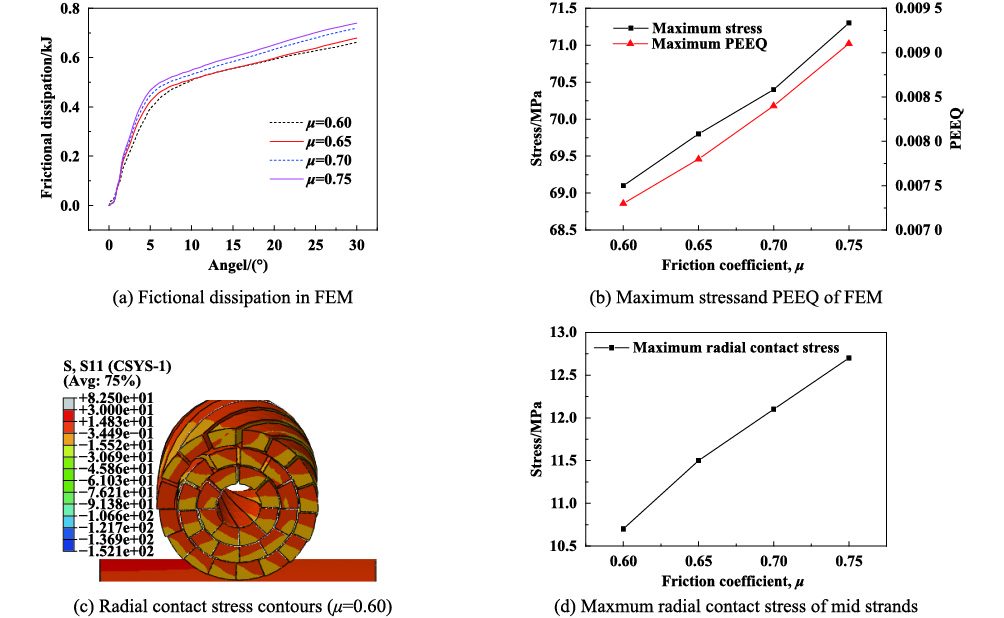
图10(a)表明股线摩擦能量损耗随着导线进入滑车的角度增加而增大，且随摩擦系数的增大而增大. 如图10(b)所示，股线最大应力与最大等效塑性应变随摩擦系数的增大呈近似线性增加. 股线摩擦损伤随摩擦系数的变化本质上是股线接触应力不同所致，图10(c)所示为D=30 d、μ=0.60条件下股线中间截面径向接触应力云图，可知中层股线同时受到外层与内层股线的挤压，尤其下部股线挤压较严重，且中层股线最大径向接触应力随摩擦系数的增大而增大[见图10(d)]，因此当股线间相对滑移量相同时，摩擦系数越大，股线滑移时磨损越严重. 由此可见，摩擦系数对股线表面的磨损、塑性变形等力学响应影响很大，当碳纤维复合芯导线通过等直径的滑车时，股线间过大的摩擦系数势必会使股线自身产生较严重的散股问题与表面磨损. 因此，导线在生产、储存等过程中应避免股线表面摩擦系数的增大，从而降低导线在架线施工过滑车时产生不必要的损伤.
![]()
图 10 不同摩擦系数下的股线摩擦行为分析结果(以D=30 d为例)Figure 10. Frictional dissipation, maximum stress and PEEQ, radial contact stress and maximum radial contact stress of strands as a function of friction coefficient determined by of FEM4. 结论
a. 导线过滑车试验后出现的散股与股线表面磨损程度随滑车底径的增大而减小，可归因于股线塑性变形与邻股的相对滑移. 股线表面以黏着磨损为主，并从初始磨损处沿股线宽度方向拓展. 初步认为滑车底径以30倍导线直径为宜.
b. 有限元模型分析表明，导线进入滑车弯曲后股线开始出现塑性变形，且股线在弯曲阶段由于相互分离与挤压导致的反复滑移使股线出现摩擦能量损耗，在理论上论证了股线损伤的产生，且塑性变形与摩擦能量损耗随滑车底径增大而减小，与试验结果一致性较好. 因此可将滑车底径D=30 d对应的股线塑性变形单元占总单元数量的32.6%作为滑车底径选取的判据.
c. 股线塑性变形与摩擦行为引起的损伤程度与自身摩擦系数有关，且随摩擦系数的增大呈近似线性增大，因此导线在生产、储存等过程中应避免股线表面摩擦系数增大导致的股线损伤.
-
![]()
图 2 导线过滑车试验照片与示意图
Figure 2. Photograph and schematic diagram of ACCC passing the stringing block test
![]()
图 6 导线中层股线外表面磨痕图
Figure 6. SEM micrographs of wear track in the outer surface of mid-layered strands
![]()
图 8 通过滑车时ACCC股线的力学响应(以D=30 d为例)
Figure 8. Mechanical response of ACCC strands when passing the stringing block (D=30 d)
![]()
图 9 不同滑车底径下ACCC股线的力学响应
Figure 9. Mechanical response of ACCC strands in different stringing blocks(D=30 d)
![]()
图 10 不同摩擦系数下的股线摩擦行为分析结果(以D=30 d为例)
Figure 10. Frictional dissipation, maximum stress and PEEQ, radial contact stress and maximum radial contact stress of strands as a function of friction coefficient determined by of FEM
表 1 710 mm2碳纤维复合芯导线几何参数[17]
Table 1 Geometric parameter of 710 mm2 ACCC
Sample Numbers Diameter/mm Section shape Stranding direction Lay ratio Strands Inner 8 d1=17.5 Trapezoid Right 15.04 Mid 12 d2=25.16 Trapezoid Left 13.09 Outer 16 d3=32.8 Trapezoid Right 10.33 Core Carbon fiber 1 dc=6.8 Circular - - Glass fiber 1 dg=9.5 Circular - - 
下载: 导出CSV
表 2 ACCC材料属性
Table 2 Material parameter of 710 mm2 ACCC
Sample Parameter E/GPa σb/MPa σs/MPa μ Strands 44 75 65 0.3 Carbon fiber 147.9 3 144.6 - 0.25 Glass fiber 53.2 1 550.0 - 0.28
下载: 导出CSV
-
[1] Middleton J, Burks B, Wells T, et al. The effect of ozone on polymer degradation in polymer core composite conductors[J]. Polymer Degradation and Stability, 2013, 98(1): 436–445
[2] Nawrocki A, Labrosse M. A finite element model for simple straight wire rope strands[J]. Computers & Structures, 2000, 77(4): 345–359
[3] Chiang Y J. Characterizing simple-stranded wire cables under axial loading[J]. Finite Elements in Analysis and Design, 1996, 24(2): 49–66
[4] Jiang W G, Warby M K, Henshall J L. Statically indeterminate contacts in axially loaded wire strand[J]. European Journal of Mechanics-A/Solids, 2008, 27(1): 69–78
[5] Raoof M, Hobbs R E. Analysis of multilayered structural strands[J]. Journal of Engineering Mechanics, 1988, 114(7): 1166–1182
[6] Zhou W, Tian H. A novel finite element model for single-layered wire strand[J]. Journal of Central South University, 2013, 20: 1767–1771
[7] Xing E, Zhou C. Analysis of the bending behavior of a cable structure under microgravity[J]. International Journal of Mechanical Sciences, 2016, 114: 132–140
[8] Fontanari V, Benedetti M, Monelli B D. Elasto-plastic behavior of a warrington-seale rope: Experimental analysis and finite element modeling[J]. Engineering Structures, 2015, 82: 113–120
[9] Kmet S, Stanova E, Fedorko G, et al. Experimental investigation and finite element analysis of a four-layered spiral strand bent over a curved support[J]. Engineering Structures, 2013, 57: 475–483
[10] Judge R, Yang Z, Jones S W, et al. Full 3D finite element modelling of spiral strand cables[J]. Construction and Building Materials, 2012, 35: 452–459
[11] Middleton J, Hoffman J, Burks B, et al. Aging of a polymer core composite conductor: Mechanical properties and residual stresses[J]. Composites Part A: Applied Science and Manufacturing, 2015, 69: 159–167
[12] Burks B, Artmentrout D, Kumosa M. Characterization of the fatigue properties of a hybrid composite utilized in high voltage electric transmission[J]. Composites Part A, 2011, 45(9): 1138–1147
[13] Hoffman J, Middleton J, Kumosa M. Effect of a surface coating on flexural performance of thermally aged hybrid glass/carbon epoxy composite rods[J]. Composites Science and Technology, 2015, 106: 141–148
[14] 蒋平海. 放线滑轮底径对滑车摩阻系数及导线磨损的影响[J]. 电力建设, 2009(1): 8–110 Jiang Pinghai. Influence of stringing block diameter on frictional coefficient and wear of ACSR[J]. Electric Power Construction, 2009(1): 8–11(in Chinese)
[15] DL/T 5284-2012. 碳纤维复合芯铝绞线施工工艺及验收导则[S]. 北京: 中国电力出版社, 2012 DL/T 5284-2012. Guide for construction and acceptance of carbon fiber complex core aluminum standed wire[S]. Beijing: China Electric Power Press, 2012(in Chinese)
[16] Q/GDW 388-2009. 碳纤维复合芯铝绞线施工工艺及验收导则[S]. 北京: 国家电网公司, 2009 Q/GDW 388-2009. Guide for construction and acceptance of carbon fiber complex core aluminum standed wire[S]. Beijing: STATE GRID Corporation of China, 2009(in Chinese)
[17] Q/GDW 1851-2012. 碳纤维复合材料芯架空导线[S]. 北京: 国家电网公司, 2013 Q/GDW 1851-2012. Overhead conductors carbon fiber composite core reinforced[S]. Beijing: STATE GRID Corporation of China, 2013(in Chinese)
[18] Waisman H, Montoya A, Betti R, et al. Load transfer and recovery length in parallel wires of suspension bridge cables[J]. Journal of Engineering Mechanics, 2010, 137(4): 227–237
[19] GB/T 228.1-2010. 金属材料拉伸试验第一部分: 温室试验方法[S]. 北京: 中国标准出版社, 2010 GB/T 228.1-2010. Metallic materials—tensile testing—part 1: method of test at room temperature[S]. Beijing: Standards Press of China, 2010(in Chinese)
[20] Burks B M, Armentrout D L, Baldwin M, et al. Hybrid composite rods subjected to excessive bending loads[J]. Composites Science and Technology, 2009, 69(15): 2625–2632
[21] 施渊吉, 黎军顽, 吴晓春, 等. 汽车法兰盘热锻模具磨损失效的实验分析和数值研究[J]. 摩擦学学报, 2016, 36(2): 215–2250 Shi Yuanji, Li Junwan, Wu Xiaochun, at al. Experimental and numerical study on the wear failureof hot forging die of automobile flange[J]. Tribology, 2016, 36(2): 215–225(in Chinese)
[22] Abdullah A B M, Rice J A, Hamilton H R, et al. An investigation on stressing and breakage response of a prestressing strand using an efficient finite element model[J]. Engineering Structures, 2016, 123: 213–224
-
期刊类型引用(7)
1. 王玉，焦亚男，谢军波，吴宁，陈利. 纺织复合材料预制体成形过程纤维束摩擦行为研究进展. 摩擦学学报. 2022(05): 874-887 . 
本站查看
2. 李勇，李健，吴蓓，张洪洲，陈晓川. 抽拔作用下棉纤维集合体压力与摩擦力的变化规律. 现代纺织技术. 2020(01): 6-10 . 百度学术
3. 马勇，夏拥军，孟凡豪. 落线高度对悬索式跨越架在断线事故下的影响分析. 噪声与振动控制. 2020(05): 59-64 . 百度学术
4. 朱院院，张晓敏，龙鹏，蒋渝. 考虑接触摩擦与各向异性性能的碳纤维复合芯导线(ACCC)径向耐压性能的有限元分析. 玻璃钢/复合材料. 2019(08): 29-34 . 百度学术
5. 周超，赵士杰. 碳纤维疏绞导线与牵引器过滑车试验及有限元分析研究. 电力科学与工程. 2019(08): 24-29 . 百度学术
6. 刘臻，董玉明，周立宪，张暕，刘龙，朱承治. 碳纤维复合芯导线过滑车散股现象. 电网与清洁能源. 2019(07): 18-23+31 . 百度学术
7. 周超，赵士杰，智鹏，刘衍平. 棒型碳纤维导线在张、弯载荷下股线受力分析. 湖北电力. 2019(04): 24-33 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 1536
- HTML全文浏览量: 496
- PDF下载量: 27
- 被引次数: 11
